Prejšnji vikend se nas je šest zbralo, da bi igrali sealed. Štirje od nas namreč kanijo ta vikend iti v Gradec na kvalifikacije za pro tour Kobe. Naš cilj je bil, da bi vsak igral z vsakim in da bi bili dvoboji razporejeni tako, da bi vsi ves čas igrali. Izkazalo se je, da tega sploh ni enostavno doseči. Za primer naj dam razpored, ki ne doseže cilja (številke ponazarjajo igralce):

Prvi krog
1 : 6
2 : 5
3 : 4

Drugi krog
1 : 4
2 : 6
3 : 5

Tretji krog
1 : 5
2 : 4
3 : 6

V četrtem krogu parov ni mogoče sestaviti tako, da bi igrali vsi in to z nasprotniki, s katerimi še niso.

Naloga se ne zdi prav zapletena, tako da me je prav jezilo, da mi ni na licu mesta uspelo sestaviti ustreznega razporeda. Doma sem si z zadevo toliko časa belil glavo, da se mi je posrečilo. Želeni razpored se dobi, če se eden od igralcev ne premika, ostalih pet pa se vsak krog krožno prestavi, kot kaže slika:

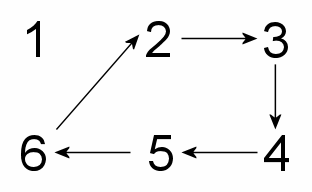
Kljub temu, da opisani razpored deluje, vseeno nisem povsem zadovoljen. Jezi me namreč, da ne najdem dobre utemeljitve, zakaj deluje, pa tudi zanima me, ali obstajajo še drugi tovrstni razporedi.